viernes, 5 de marzo de 2010

Las principales propiedades de la media aritmética son:

Propiedades

  • Su cálculo es muy sencillo y en él intervienen todos los datos.
  • Su valor es único para una serie de datos dada.
  • Se usa con frecuencia para comparar poblaciones, aunque es más apropiado acompañarla de una medida de dispersión.
  • Se interpreta como "punto de equilibrio" o "centro de masas" del conjunto de datos, ya que tiene la propiedad de equilibrar las desviaciones de los datos respecto de su propio valor:
\frac{\sum_{i=1}^n (x_i-\overline{x})}{n} = \frac{\sum_{i=1}^n x_i}{n} - \frac{\sum_{i=1}^n \overline{x}}{n} = \overline{x} - \overline{x} = 0
  • Minimiza las desviaciones cuadráticas de los datos respecto de cualquier valor prefijado, esto es, el valor de 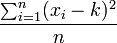\frac{\sum_{i=1}^n (x_i-k)^2}{n} es mínimo cuando k = \overline{x}. Este resultado se conoce como Teorema de König. Esta propiedad permite interpretar uno de los parámetros de dispersión más importantes: la varianza.
xi' = axi + b entonces 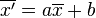\overline{x'} = a \overline{x} + b, donde 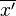\overline{x'} es la media aritmética de los xi', para i = 1, ..., n y a y b números reales.

Inconvenientes de su uso

Este parámetro, aún teniendo múltiples propiedades que aconsejan su uso en situaciones muy diversas, tiene también algunos inconvenientes, como son:

  • Para datos agrupados en intervalos (variables continuas) su valor oscila en función de la cantidad y amplitud de los intervalos que se consideren.
La estatura media como resumen de una población homogénea (abajo) o heterogénea (arriba).
  • Es una medida a cuyo significado afecta sobremanera la dispersión, de modo que cuanto menos homogéneos sean los datos, menos información proporciona. Dicho de otro modo, poblaciones muy distintas en su composición pueden tener la misma media. Por ejemplo, un equipo de baloncesto con cinco jugadores de igual estatura, 1,95 m, evidentemente, tendría una estatura media de 1,95 m, valor que representa fielmente a esta población homogénea. Sin embargo, un equipo de jugadores de estaturas más heterogéneas, 2,20 m, 2,15 m, 1,95 m, 1,75 m y 1,70 m, por ejemplo, tendría también, como puede comprobarse, una estatura media de 1,95 m, valor que no representa a casi ninguno de sus componentes.
  • En el cálculo de la media no todos los valores contribuyen de la misma manera. Los valores altos tienen más peso que los valores cercanos a cero. Por ejemplo, en el cálculo del salario medio de un empresa, el salario de un alto directivo que gane 1.000.000 de € tiene tanto peso como el de diez empleados "normales" que ganen 1.000 €. En otras palabras, se ve muy afectada por valores extremos.
  • No se puede determinar si en una distribución de frecuencias hay intervalos de clase abiertos.

Media aritmética ponderada

A veces puede ser útil otorgar pesos o valores a los datos dependiendo de su relevancia para determinado estudio. En esos casos se puede utilizar una media ponderada.

Si x1,x2,...,xn son nuestros datos y w1,w2,...,wn son sus "pesos" respectivos, la media ponderada se define de la siguiente forma:

\frac{x_{1}w_{1}+x_{2}w_{2}+ ...+x_{n}w_{n}}{w_{1}+w_{2}+ ...+w_{n}}

Media muestral

Esencialmente, la media muestral es el mismo parámetro que el anterior, aunque el adjetivo "muestral" se aplica a aquellas situaciones en las que la media aritmética se calcula para un subconjunto de la población objeto de estudio.

La media muestral es un parámetro de extrema importancia en la inferencia estadística, siendo de gran utilidad para la estimación de la media poblacional, entre otros usos.

Publicado por en

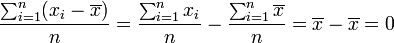
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)