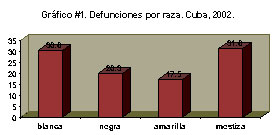
Cada clase se representa con una barra o rectángulo cuya altura (si el eje de frecuencias es el vertical) resulta proporcional a la frecuencia que representa. Todas las barras deben tener el mismo grosor y el espacio entre barras debe ser el mismo, teniendo un ancho de 0,5 a 1 vez el de las barras.
El orden de las barras en el gráfico debe ser el mismo que en la tabla que le sirve de fuente. Por ello, si no existe un criterio 'a priori' de orden entre las clases establecidas, pueden ordenarse las mismas (y, como es lógico, las barras en el gráfico) en orden ascendente o descendente de las frecuencias, para facilitar la interpretación de esos resultados.
b) Gráfico circular, de sectores o pastel.
El gráfico siguiente es un ejemplo típico de gráfico circular (confeccionado con los mismos valores del gráfico anterior):
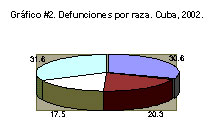
Se usa, fundamentalmente, para representar distribuciones de frecuencias relativas (%) de una variable cualitativa o cuantitativa discreta. En este gráfico se hace corresponder la medida del ángulo de cada sector con la frecuencia correspondiente a la clase en cuestión. Si los 360º del círculo representan el 100 % de los datos clasificados, a cada 1% le corresponderán 3,6º. Luego, para obtener el tamaño del ángulo para un sector dado bastaría con multiplicar el por ciento correspondiente por 3,6º (por simple regla de tres).
Mediante un sector circular se representan las medidas angulares correspondientes a las diferentes categorías, respetando el orden establecido en la tabla, partiendo de un punto dado de la circunferencia. Ese punto dado generalmente es el punto más alto de la circunferencia (12 en el reloj). Si lo que se representa en cada sector no puede colocarse dentro del mismo, se elabora una leyenda o se coloca fuera, adyacente al mismo. Se acostumbra a diferenciar los sectores con tramas o colores diferentes, lo que hace que resulte un gráfico más vistoso que el de barras simples.
c) Gráfico de barras múltiples.
Veamos un ejemplo de este tipo de gráfico:
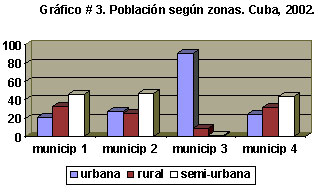
Este es un gráfico de barras triples. En la leyenda aparece el criterio de clasificación que complementa al que aparece en el eje de categorías. Note la separación entre los “tríos” de barras.
d) Gráfico de barras compuestas.
Su objetivo es la representación de las frecuencias relativas (%) observadas en clasificaciones dobles, es decir, cuando son dos los criterios de clasificación, para variables cualitativas o cuantitativas discretas.
Su forma de construcción es la siguiente: cada barra representa el 100 % de los individuos en cada clase del criterio principal de clasificación y se divide, proporcionalmente, en los por cientos correspondientes a las clases del otro criterio de clasificación. Como es lógico, las diferentes partes en que se dividen las barras compuestas se diferencian con tramas o colores diferentes.
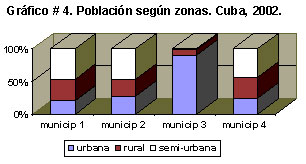
Este gráfico se usa para representar una distribución de frecuencias de una variable cuantitativa continua.
Habitualmente se representa la frecuencia observada en el eje Y, y en el eje X la variable. La escala del eje correspondiente a la variable se rotula con los límites inferiores de notación de las clases consideradas y se agrega al final el que le correspondería a una clase subsiguiente inexistente. En este caso, las frecuencias deben resultar proporcionales no a la altura de las barras, sino al área de las mismas, lo que significa que la obtención de las alturas de las barras resulta un poco más compleja que en los gráficos anteriores. Además, las barras van contiguas y no separadas, por la naturaleza continua de la variable de clasificación.
Para lograr la proporcionalidad entre la frecuencia y el área de la barra que esta representa el procedimiento es el siguiente: sabemos que el área de un rectángulo es el producto de la base por la altura y que la base de una barra en el gráfico es, precisamente, la amplitud del intervalo de clase, luego la formulación de esa 'proporcionalidad' sería:
frecuencia observada = amplitud del intervalo* altura de la barra
Conocemos la frecuencia observada y la amplitud de cada uno de los intervalos, por tanto, para calcular las alturas de las barras sólo se tendría que despejar en la fórmula correspondiente, lo que quedaría:
altura de la barra = frecuencia observada / amplitud del intervalo
Debido a la forma de obtención de esas alturas, el eje de las frecuencias debe rotularse como número de individuos por unidad de medida de la variable en cuestión, por ejemplo: 'defunciones por año de edad'; 'número de individuos por kg de peso; etc.
El procedimiento que hemos explicado es el general, pero sucede, en el caso particular de que las amplitudes de todos los intervalos de clase sean iguales, que no es estrictamente necesario realizar estos cálculos: sería dividir todas las frecuencias por una constante y eso no alteraría el gráfico, pues se mantendría la misma relación de proporcionalidad entre las frecuencias.
Veámoslo a través de un ejemplo, cuando las amplitudes de los intervalos son iguales: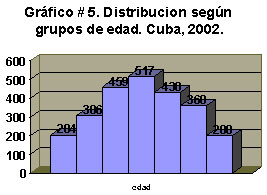
En este caso se usó la frecuencia absoluta como altura de la barra. Todas las barras tienen el mismo ancho y van unidas, una a continuación de la otra, porque están representando una variable continua (edad).
Es sencillo darse cuenta de que es imposible presentar otra distribución en ese gráfico, pues unas barras podrían ocultar a otras. Es decir, este tipo de gráfico sólo es útil para presentar una distribución.
Se utiliza, al igual que el histograma, para representar distribuciones de frecuencias de variables cuantitativas continuas, pero como no se utilizan barras en su confección sino segmentos de recta, de ahí el nombre de polígono. Habitualmente se usa cuando se quiere mostrar en el mismo gráfico más de una distribución o una clasificación cruzada de una variable cuantitativa continua con una cualitativa o cuantitativa discreta, ya que por la forma de construcción del histograma sólo se puede representar una distribución.
Para su confección, una vez construidas y rotuladas las escalas, de manera similar a como se realiza para un histograma, los valores de alturas obtenidos se plotean sobre el punto medio o marca de clase de los intervalos correspondientes y luego se procede a unir esos puntos con segmentos de recta.
Veamos un ejemplo de polígono de frecuencias:
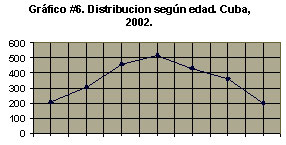
g) Gráfico de frecuencias acumuladas u ojiva.
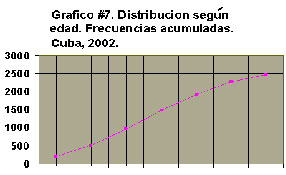
La diferencia con el polígono de frecuencia es que la frecuencia acumulada no se plotea sobre el punto medio de la clase, sino al final de la misma, ya que representa el número de individuos acumulados hasta esa clase. Como el valor de la frecuencia acumulada es mayor a medida que avanzamos en la distribución, la poligonal que se obtiene siempre va a ser creciente y esa forma particular de la misma es la que ha hecho que se le dé también el nombre de ojiva.
Este es uno de los más sencillos de confeccionar. Su uso estadístico fundamental es en la representación de series cronológicas, y en casos particulares, como el del Crecimiento y Desarrollo Humanos, para representar los valores promedio o posicionales (medias, medianas y percentiles, que se estudiarán más adelante) de muchas dimensiones: peso para la edad, peso para la talla y talla para la edad, entre otras.
Uno de los ejes (habitualmente el horizontal) se usa para la unidad de tiempo estudiada: años, días, etc.. En el otro eje se representa la frecuencia o el indicador calculado a partir de esos datos. En este tipo de gráfico es particularmente importante la relación de proporcionalidad entre los ejes para evitar malas interpretaciones del fenómeno que se presenta.
El gráfico que sigue es un ejemplo de gráfico de este tipo:
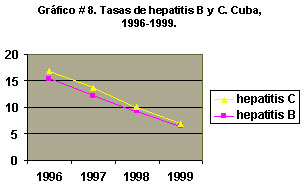
En el mismo gráfico se puede presentar más de una serie de datos si la escala usada se adecua para todas, cuando los valores de las mismas no son extremadamente diferentes.

No hay comentarios:
Publicar un comentario